To gain practice with building data products end-to-end, I recently developed a product classification API. The API helps classify products based on its title—instead of figuring out which category your product belongs to (out of thousands), you can provide the title and the API returns the top 3 most likely categories. (Github repositiory)

Update: API discontinued to save on cloud cost.

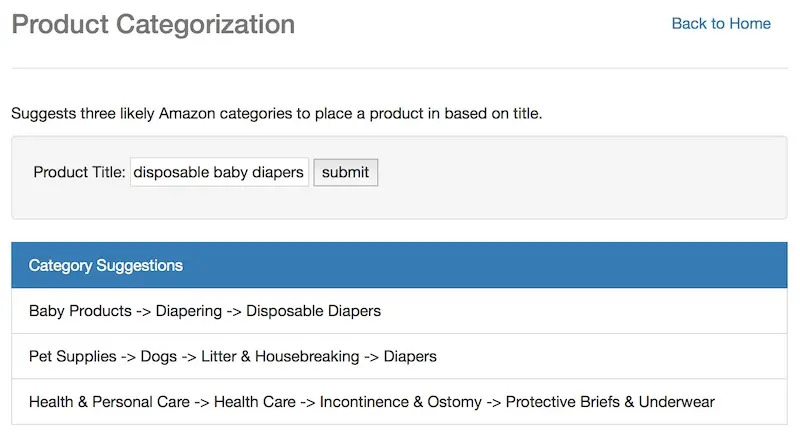
Input: Title. Output: Suggested categories.

This is part of a series of posts on building a product classification API:

• Data acquisition and formatting (part 1)
• Data cleaning and preparation (part 2)
• App development (part 3)
• Image classification demo
• Image search demo

Where did I get the product data from?

I initially intended to build a web scraper to collect product data from Amazon’s and Alibaba’s sites. However, I figured this (skill) was not absolutely necessary, especially at work—product data would be stored and available in databases. In addition, the process of scraping and structuring scraped data was estimated to take up at least 30% of overall effort. Thus, I decided to use open-sourced product data instead.

It was surprisingly difficult to find good quality open-sourced product data. I was on the verge of building a scraper when I stumbled upon Julian McAuley’s site: http://jmcauley.ucsd.edu/data/amazon/. Acknowledgements to Julian and his team for the Amazon product data used to build this API.

For this project, we’ll be using the product metadata, containing 9.4 million products (3.1gb zipped). As we’ll see, after cleaning and preparation, only a fraction is usable for training a product classification model for the API.

How does the product metadata look like?

The metadata contains the following fields:

• asin: Product ID
• title: Product name
• price: Product price (in USD)
• imUrl: Product image url
• related: Related products (that Amazon recommends; e.g., “also bought”, “also viewed”, “bought together”, etc)
• salesRank: Product rank in top-level category (based on number of sales over a period)
• brand: Product brand
• categories: List of categories the product belongs to

Here’s how a product would look like in the original json format. I’ll be using this example throughout this post.

{
 "asin": "B0147ZZKQ2",
 "title": "Onitsuka Tiger Ultimate 81 Running Shoe",
 "price": 68.88,
 "imUrl": "http://ecx.images-amazon.com/images/I/51fAmVkTbyT._SY300_.jpg",
 "related":
 {
  "also_bought": ["B00JHONN1S", "B002BZX8Z6", "B00D2K1M3O", "0000031909", "B00613WDTQ", "B00D0WDS9A", "B00D0GCI8S", "0000031895", "B003AVKOP2", "B003AVEU6G"],
  "also_viewed": ["B002BZX8Z6", "B00JHONN1S", "B008F0SU0Y", "B00D23MC6W", "B00AFDOPDA", "B00E1YRI4C", "B002GZGI4E", "B003AVKOP2", "B00D9C1WBM", "B00CEV8366"],
  "bought_together": ["B002BZX8Z6"]
 },
 "salesRank": {"Clothing, Shoes & Jewelry": 1368},
 "brand": "Onitsuka",
 "categories": [["Clothing, Shoes & Jewelry", "Men", "Shoes", "Fashion Sneakers"], ["Sports & Outdoors", "Exercise & Fitness", "Running", "Footwear"]]
}

Converting the JSON to CSV format

The json data comes zipped. Here’s how we can read it into a pandas dataframe (and save to csv, if necessary):

import pandas as pd
import gzip

def parse(path):
    g = gzip.open(path, 'rb')
    for l in g:
    yield eval(l)

def get_df(path):
    i = 0
    df = {}
    for d in parse(path):
        df[i] = d
        i += 1
    return pd.DataFrame.from_dict(df, orient='index')

df = get_df('metadata.json.gz')

df.to_csv('metadata_csv', index=False)

The above approach reads the entire dataset and loads it into a dataframe. This is viable given the small data size (3.1gb). However, for larger datasets ( >100gb), we’ll need an alternative approach. One way is to read the zipped json and write to csv, row by row:

import json
import gzip
import csv

def parse(path):
    g = gzip.open(path, 'rb')
    for l in g:
       yield eval(l)

def json_to_csv(read_path, write_path):
    csv_writer = csv.writer(open(write_path, 'w'))
    i = 0
    for d in parse(read_path):
        if i == 0:
            header = d.keys()
            csv_writer.writerow(header)
        i += 1
    csv_writer.writerow(d.values())

json_to_csv('metadata.json.gz', 'metadata.csv')

Formatting and cleaning the category data

Now that we’ve parsed the product data into a dataframe (and saved it to csv), we can begin working with the category data. Here’s how the category data for the Onitsuka Tiger shoes looks like:

[["Clothing, Shoes & Jewelry", "Men", "Shoes", "Fashion Sneakers"],
["Sports & Outdoors", "Exercise & Fitness", "Running", "Footwear”]]

The shoes are listed under two categories: “Clothing, Shoes, and Jewelry” (CSJ) and “Sports & Outdoors” (S&O). This means they are cross-listed across both categories, ensuring they can be found if you browse either the CSJ or the S&O catalogue. (Yes, they’re so badass they qualify as both fashion sneakers and running footwear; check out the top review here: Whappoww!! Ninja sneaks for bosses of chill)

The API will classify a product into its primary category (i.e., the first category provided), ensuring a one-to-one relationship between products and their respective categories. Often, guidelines exist for which category should be the primary one (e.g., Shoes should have CSJ categories as their primary category)

Converting category data into category path strings

First, we’ll parse the category from a list of lists to a string. Simultaneously, we’ll keep only the primary categories (i.e., first category in the list). After parsing, this is the resulting category:

"Clothing, Shoes & Jewelry -> Men -> Shoes -> Fashion Sneakers"

Note: My preference is to convert the category data into a category path, a single string connected by arrows (->). However, any format should work fine.

Here’s the code to how it’s done:

def get_category_path(category_path_list):
    """
    (Str of list of list(s)) -> str

    Returns the category path given a string of list of lists of 
    categories. If there are more than one list of categories provided, 
    returns the category path from the first list.

    >>> get_category_path("[['A', 'B', 'C'], ['D', 'E', 'F', 'G']]")
    'A -> B -> C'
    >>> get_category_path("[['P1', 'P2', 'P3', 'P4']]")
    'P1 -> P2 -> P3 -> P4'

    :type category_path_list: str
    :param category_path_list: A string containing a list of at least 
    one list of categories
    :return: A string showing the full category path of the FIRST 
    category in the list (assumed to be primary category)
    """
    try:
        return ' -> '.join(eval(category_path_list)[0])
    except IndexError: # Error if the outer list is empty
        return 'no_category'
    except TypeError: # Error if the outer list is missing
        return 'no_category'

# Create column for category path
df['category_path'] = df['categories'].apply(get_category_path)

Exclude data where title or category is missing

If either the title or category is missing, we won’t be able to use the product data to train our model. Thus, we’ll exclude products with incomplete data, as such:

df.dropna(subset=['title'], inplace=True)
df = df[df['category_path'] != 'no_category']

We started with 9.43 million products. More than 1 million have either missing title or category, leaving us with 7.98 million products.

Exclude certain categories

There are some categories of products where the title does not provide any information about the product category (e.g., Books, Movies, etc). These products are usually classified via alternative approaches. For example, the availability of ISBN data indicates the product is a book, while the availability of ratings (e.g., PG-13) indicates the product is a movie.

We’ll exclude certain categories of products as follows, leaving us with 5.59 million products:

df = df[df['category_path_lvl1'] != 'Books']
df = df[df['category_path_lvl1'] != 'CDs & Vinyl']
df = df[df['category_path_lvl1'] != 'Movies & TV']

Note: You may have noticed that the code above filters on the column category_path_lvl1. This column contains the top level categories for products (e.g., “Electronics”, “Clothing, Shoes, and Jewelry”, Sports & Outdoors”). I’ll leave deriving this as an exercise for the audience ;)

Exclude non-deepest/non-narrowest categories

In the list of categories, we’ll find some that seem to stop halfway, such as the first category path below:

"Clothing, Shoes & Jewelry -> Men -> Shoes"
"Clothing, Shoes & Jewelry -> Men -> Shoes -> Fashion Sneakers"

In this case, the latter category is deeper (and narrower) than the former. Classifying products to the deepest category helps shoppers find relevant products easier (given that the category is narrower). Thus, we’ll exclude products that are not at the deepest category.

Here’s one way to do it. We’ll first sort the categories and compare each category path with the next. If the category path is not in the next (i.e., the category path is not a substring of the next category), then it is a deepest category and we append it to a list. We’ll then keep only products with categories in our list.

# Create df of category path counts
category_path_df = df.groupby('category_path').agg({'title': 'count'}).sort_values(by='title', ascending=False).reset_index()

category_path_df.sort_values(by='category_path', inplace=True)
category_path_df['category_path_next'] = category_path_df['category_path'].shift(-1)
category_path_df.fillna('no_comparison', inplace=True)

# Create list of category_paths which are deepest category
category_path_list = []
for i, value in category_path_df.iterrows():
    category_path = value['category_path']
    category_path_next = value['category_path_next']
    if category_path not in category_path_next:
        category_path_list.append(category_path)

# Create df of category_path
category_path_df = pd.DataFrame(category_path_list, columns=['category_path'])

# Keep only rows where the category is in category_df
df = df[df['category_path'].isin(category_path_df['category_path'])]

Initially, we had 17.6 k categories. After excluding non-deepest categories, about 15 k categories (and 4.61 mil products) remain.

Exclude categories that have too few products

Lastly, to ensure sufficient data to split into train and test sets, and train our model, we’ll exclude categories with less than 10 products. With a 50-50 train-test split, we’ll have at least five products to train per category. This shouldn’t be too difficult and I encourage you to try it out yourself.

After excluding products based on this condition, we’re left with 4.59 mil products.

And we’re done!

Congratulations on making it this far!

We’re done with the key steps to cleaning the category data. There may also be other cleaning involved, such as excluding temporary categories (i.e., “Black Friday Sales”, “11-11 Sales”, etc) but we shall not cover them.

As shown, there’s a lot of work to be done in acquiring, formatting, and cleaning of the data before we get to building a model to classify products. In this case, I’m thankful to Julian McAudley and his kind sharing of the Amazon product metadata.

In the next article, we go into—yeap, you guessed it—more data cleaning and preparation (specific to titles). This basic data preparation is key to training our classifier with high accuracy.

p.s., I would greatly appreciate any feedback on process, code, writing style, etc in the comments below. Thank you!

If you found this useful, please cite this write-up as:

Yan, Ziyou. (Oct 2016). Product Classification API Part 1: Data Acquisition. eugeneyan.com. https://eugeneyan.com/writing/product-categorization-api-part-1-data-acquisition-and-formatting/.

or

@article{yan2016acquisition,
  title   = {Product Classification API Part 1: Data Acquisition},
  author  = {Yan, Ziyou},
  journal = {eugeneyan.com},
  year    = {2016},
  month   = {Oct},
  url     = {https://eugeneyan.com/writing/product-categorization-api-part-1-data-acquisition-and-formatting/}
}