Is accuracy the only metric that matters in recommendation systems?

Maybe not.

Imagine you started using Spotify to listen to your favourite artiste. If Spotify only recommended music from that artiste, would it be accurate? Yes. Would you like those recommendations? Probably at the start, but you would get bored quickly.

Don't bore your users (and their cats) with your recommendations

What you want is for a recommender system to (pleasantly) surprise you. That is the concept of serendipity.

Why are accuracy (aka relevance) metrics more commonly discussed and applied then?

I suspect it’s due to a combination of the following:

• Accuracy metrics (e.g., NDCG, MAP, AUC, recall@n) are widely available in libraries (e.g., sklearn, SparkML); implementations for serendipity metrics are scarce.
• Accuracy metrics are more commonly taught in classes, to significant depth; serendipity metrics are mostly touch-and-go.
• Accuracy metrics are universally adopted in literature; the jury’s still out on formula for serendipity metrics.
• During offline evaluation, it is easier to improve accuracy metrics.
• In production, accuracy metrics have a stronger correlation with (short-term) recommender performance (i.e., click-through-rate, conversion).

Nonetheless, if you’re keen to learn about an alternative approach to evaluating recommender systems (based on what I gleaned from 10+ papers), read on.

Why serendipity?

It keeps your customers interested.

In the earlier example, the music recommender was very accurate—it only recommended music from artistes you liked and previously listened to. A model solely focused on accuracy would do very well in offline evaluation (of the latest week of data).

But in the real world, it would suck. It would recommend very similar music daily. Users would get bored soon.

People intrinsically enjoy variety and discovering things such as new artistes, genres, communities, etc. Helping users discover new products keeps them interested.

It’s good for business.

Keeping customer utility high is important. But besides customer utility, you also need to care about assortment health and seller health.

From an e-commerce perspective, poor assortment health means a small percentage of products, categories, or sellers (5%) get a disproportionately large portion of sales and revenue (95%). If those top sellers decide to move to a competitor platform, it’s gonna hurt. The same would happen if a top-selling product stops being available (e.g., out of stock, banned, cease production).

Introducing serendipity (and the associated metrics of diversity and novelty) help recommend more products from the long-tail of assortment. This distributes sales more evenly, reducing dependency and risk on the minority of products and sellers.

As a plus, you get to expose long-tail and cold-start products to customers. This helps gather training data which you can use to improve your recommender. It’s a virtuous cycle.

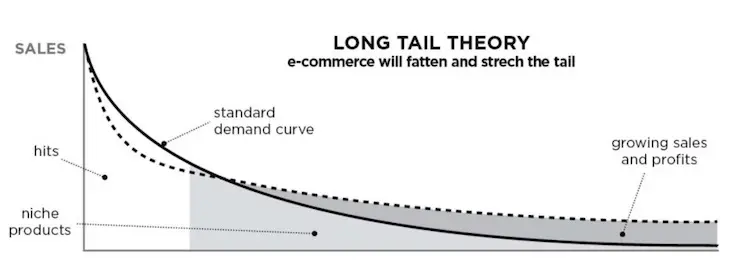
Stretching the long tail

How to measure serendipity?

“If you can’t measure it, you can’t improve it” - Peter Drucker

Unfortunately, there’s no industry agreed-upon standard to measure serendipity. Unlike relevance metrics such as non-discounted cumulative gain (NDCG), mean average precision (MAP), recall, precision, etc.

To gain a better understanding of how to measure serendipity, I went through 10+ papers on serendipity in recommender systems. Here’s a summary of the key metrics and the various ways to measure them.

Diversity

Diversity measures how narrow or wide the spectrum of recommended products are. A recommender that only recommends the music of one artiste is pretty narrow; one that recommends across multiple artistes is more diverse.

There are two main ways of measuring diversity—based on item and based on users.

Measuring diversity based on item is straightforward. We can do this based on metadata of the recommended items:

• How many different categories/genres?
• How many different artistes/authors/sellers?
• What is the kurtosis (“tailness”) of the price distribution?
• How different (i.e., distant) are the product embeddings?

Another approach is measuring diversity based on existing customers. For each item in the recommended set, who has consumed it? If the items have a relatively large proportion of common users, the recommended items are likely very similar.

One way to measure this is cosine similarity (Ziegler et al., 2004). For two products, what’s the proportion of common users?

This can then be extended to the set of recommended items.

Novelty

Novelty measures how new, original, or unusual the recommendations are for the user.

In general, recommendations will mostly consist of popular items because (i) popular items have more data and (ii) popular items do well in offline and online evaluations.

However, if an item is popular or top-selling, a user would already have been exposed to it. This could happen via your “top-selling” or “trending” banners, social media, or a user’s relationships (i.e., family, friends, co-workers). Therefore, it makes sense to tweak a recommender for novelty to reduce the number of popular items it recommends.

The common way I’ve seen papers measure novelty is to compare a user’s recommended items to the population. How often does a user’s recommendations occur in the rest of the population’s recommendations? There are two forms of measuring this (Zhang et al 2011, Vargas & Castells, 2011):

In both equations, the numerator counts the number of users who were recommended the item. The denominator counts the total number of users. In both cases, if all users were recommended the item, then novelty would be zero.

Some papers measure novelty this way, comparing a user’s recommendations against the population’s recommendations. I’m not sure if this is the best approach to measure novelty—how does it matter to the user what recommendations other people receive?

If a user is the only person recommended a product (e.g., a Harry Potter book), novelty—as measured above—would be close to maximum.

But the rest of the population might already have purchased/read the book (and thus not be recommended it). If everyone around the user has bought, read, or talked about the product—is the recommended product still novel to the user?

A better measure of novelty is to consider the population’s interactions (e.g., purchases, clicks) instead of recommendations. This reflects how likely the user has been exposed to the product based on the population historical engagement.

What if we want to measure novelty specific to a user? Most literature refers to that as unexpectedness or surprise.

Unexpectedness (aka surprise)

One measure of unexpectedness is to compare a user’s new recommendations (from an updated recommender) against previous recommendations. This measures “how much surprise are we introducing with this serendipity feature”. It’s useful for tracking incremental improvements on recommendation systems.

Another approach is to compare recommendations relative to the user’s historical item interaction. This measures “how surprising are these recommendations given what the user previously bought/clicked on”. I believe this is a better way to operationalise surprise.

One way to measure this is via point-wise mutual information (PMI). PMI indicates how similar two items are based on the number of users who have purchased both items and each item separately (similar to measuring diversity based on users).

p(i) is the probability of any user consuming item I, while p(i, j) is the probability of a user consuming both. PMI ranges from -1 to 1, where -1 indicates that the two items are never consumed together.

Another approach is to consider some distance metric (e.g., cosine similarity). We compute cosine similarity between a user’s recommended items (I) and historical item interactions (H). Lower cosine similarity indicates higher unexpectedness.

Serendipity

Serendipity is measured as unexpectedness multiplied by relevance, where relevance is 1 if the recommended item is interacted with (e.g., purchase, click) and 0 otherwise. For a recommended item (i), we only consider unexpectedness if the user interacted with i.

To get overall serendipity, we average over all users (U) and all recommended items (I).

It seems straightforward to implement this in code but in reality, it’s a tricky matter. If your recommender system is deliberately introducing long-tail and cold-start products, you can expect the relevance metric to perform poorly in offline evaluations. Nonetheless, the recommendations might still be useful to customers and perform well in an A/B test.

(In a previous project where I deliberately introduced cold-start products in a product ranking system, the offline evaluation metrics were bad and we expected conversion to drop a bit. To our surprise, we actually saw conversion improve during the A/B test.)

So take offline evaluation metrics of serendipity (and relevance) with a pinch of salt. Use them to compare between multiple recommenders but don’t let them dissuade you from starting an A/B test.

Putting it all together

Whew! That was a lot of material and formula. How do I know which to use and when?

Here are some basic guidelines:

Diversity

• Do you care about how different the recommended items look? If so, measure diversity based on item features.
• Do you care about the cross-pollination of communities and user groups (e.g., Facebook group and meet-up group recommendations)? If so, consider diversity based on users.

Novelty

• Do you want a user’s recommendations to be different from what their friends get? If so, compare between a user’s and population’s recommendations.
• Do you want a user’s recommendations to be novel relative to historical public interaction? If so, compare a user’s recommendations vs the population’s past purchase/clicks.

Unexpectedness

• Do you want to surprise users with recommendations that are different from what they are used to? If so, compare between a user’s new and previous recommendations.
• Do you want to surprise users with recommendations that are different from the products they have previously purchased? If so, compare between a user’s recommendations to their past purchase.

Conclusion

Measuring serendipity and her cousin metrics isn’t easy or straightforward. You can’t simply import them from a library (e.g., sklearn, SparkML), unlike NDCG, MAP, etc.

Nevertheless, tracking serendipity is useful for a successful long-term recommendation strategy. Too much focus on accuracy leads to boring recommendations, bored users, poor assortment health, and suboptimal business.

What other approaches do you use to evaluate recommendation engines? Reach out via Twitter (@eugeneyan) or share in the comments below!

References

Adomavicius, G., & Kwon, Y. (2011, October). Maximizing aggregate recommendation diversity: A graph-theoretic approach. In Proc. of the 1st International Workshop on Novelty and Diversity in Recommender Systems (DiveRS 2011) (pp. 3-10).

Celma, Ò., & Herrera, P. (2008, October). A new approach to evaluating novel recommendations. In Proceedings of the 2008 ACM conference on Recommender systems (pp. 179-186).

Chen, L., Wang, N., Yang, Y., Yang, K., & Yuan, Q. (2019). User Validation of Recommendation Serendipity Metrics. arXiv preprint arXiv:1906.11431.

Ge, M., Delgado-Battenfeld, C., & Jannach, D. (2010, September). Beyond accuracy: evaluating recommender systems by coverage and serendipity. In Proceedings of the fourth ACM conference on Recommender systems (pp. 257-260).

Iaquinta, L., De Gemmis, M., Lops, P., Semeraro, G., Filannino, M., & Molino, P. (2008, September). Introducing serendipity in a content-based recommender system. In 2008 Eighth International Conference on Hybrid Intelligent Systems (pp. 168-173). IEEE.

Kotkov, D., Konstan, J. A., Zhao, Q., & Veijalainen, J. (2018, April). Investigating serendipity in recommender systems based on real user feedback. In Proceedings of the 33rd Annual ACM Symposium on Applied Computing (pp. 1341-1350).

Kotkov, D., Wang, S., & Veijalainen, J. (2016). A survey of serendipity in recommender systems. Knowledge-Based Systems, 111, 180-192.

Lee, K., & Lee, K. (2015). Escaping your comfort zone: A graph-based recommender system for finding novel recommendations among relevant items. Expert Systems with Applications, 42(10), 4851-4858.

Mourão, F., Fonseca, C., Araujo, C. S., & Meira Jr, W. (2011, October). The Oblivion Problem: Exploiting Forgotten Items to Improve Recommendation Diversity. In DiveRS@ RecSys (pp. 27-34).

Oku, K., & Hattori, F. (2011). Fusion-based Recommender System for Improving Serendipity. DiveRS@ RecSys, 816, 19-26.

Panagiotis, A., & Alexander, T. (2011). On unexpectedness in recommender systems: Or how to expect the unexpected. In Workshop on Novelty and Diversity in Recommender Systems, 2011.

Santini, S., & Castells, P. (2011). An evaluation of novelty and diversity based on fuzzy logic. In CEUR Workshop Proceedings. Pablo Castells.

Vargas, S., & Castells, P. (2011, October). Rank and relevance in novelty and diversity metrics for recommender systems. In Proceedings of the fifth ACM conference on Recommender systems (pp. 109-116).

Zhang, Y. C., Séaghdha, D. Ó., Quercia, D., & Jambor, T. (2012, February). Auralist: introducing serendipity into music recommendation. In Proceedings of the fifth ACM international conference on Web search and data mining (pp. 13-22).

Thanks to Xinyi Yang and Gabriel Chuan for reading drafts of this.

If you found this useful, please cite this write-up as:

Yan, Ziyou. (Apr 2020). Serendipity: Accuracy’s Unpopular Best Friend in Recommenders. eugeneyan.com. https://eugeneyan.com/writing/serendipity-and-accuracy-in-recommender-systems/.

or

@article{yan2020serendipity,
  title   = {Serendipity: Accuracy’s Unpopular Best Friend in Recommenders},
  author  = {Yan, Ziyou},
  journal = {eugeneyan.com},
  year    = {2020},
  month   = {Apr},
  url     = {https://eugeneyan.com/writing/serendipity-and-accuracy-in-recommender-systems/}
}